Produktionsplanung mit Timefold – Wenn intelligente Algorithmen den Takt der Maschinen bestimmen

Teil 1 der Serie „Optimierungsprobleme in der Praxis“
In dieser Serie zeige ich, wie sich reale Planungs- und Entscheidungsprobleme mit modernen Optimierungstools wie Timefold elegant lösen lassen – praxisnah, reproduzierbar und mit klarem Mehrwert für Unternehmen.

Wenn Planung zum Puzzle wird

In der Theorie klingt Produktionsplanung einfach: ein paar Maschinen, ein Dutzend Aufträge – und man muss nur entscheiden, wer wann was bearbeitet, richtig?

In der Praxis ist das ein Alptraum aus Abhängigkeiten. Ein Auftrag darf erst starten, wenn ein anderer fertig ist. Manche Maschinen sind schneller, andere günstiger. Und natürlich gibt es Liefertermine, Rüstzeiten und Prioritäten.

Was zunächst wie eine einfache Zuordnungsaufgabe wirkt, entpuppt sich schnell als hochkomplexes Zusammenspiel vieler Variablen. Der Versuch einer manuellen Lösung kann dann schnell zum Problem werden.

Von der Intuition zur Optimierung

Viele Unternehmen lösen solche Probleme erstaunlich „analog“, z.B. mit Excel-Tabellen, Bauchgefühl (Erfahrung) oder festen Regeln („immer erst die dringenden Jobs“). Diese Lösungen funktionieren, solange alles klein und überschaubar bleibt.

Doch sobald das System komplexer wird, steigt die Zahl der möglichen Kombinationen schnell. Und genau hier setzen wir an: statt manuell zu planen, beschreiben wir das Problem formal, und ein Solver sucht systematisch nach der besten Kombination.

Timefold, das Open-Source-Tool, das ich in dieser Serie verwende, ist genau dafür gemacht.
Es ist kein Machine-Learning-System, sondern ein Constraint-Solver: er „lernt“ nicht aus Daten, sondern optimiert innerhalb von Regeln. Der Begriff Optimierung ist hier eigentlich nicht ganz präzise. Ziel ist es nicht, das absolute Optimum zu finden, sondern innerhalb einer vertretbaren Zeit eine sehr gute Lösung zu ermitteln. Dazu nutzt Timefold heuristische Verfahren, die in der Praxis meist deutlich bessere Ergebnisse liefern als jede manuelle oder intuitive Planung.

Das Beispiel: Produktionsplanung im Miniaturformat

Nehmen wir ein vereinfachtes Beispiel:
Ein kleiner Fertigungsbetrieb hat vier Maschinen und aktuell drei Aufträge mit insgesamt zehn Arbeitsschritten. Jeder Arbeitsschritt hat eine Bearbeitungszeit und kann nur auf bestimmten Maschinen laufen. Die Reihenfolge der Arbeitsschritte wird durch den jeweiligen Auftrag vorgegeben.

Das Ziel ist einfach: Minimiere die Gesamtdauer, bis alle Jobs fertig sind – den sogenannten Makespan.

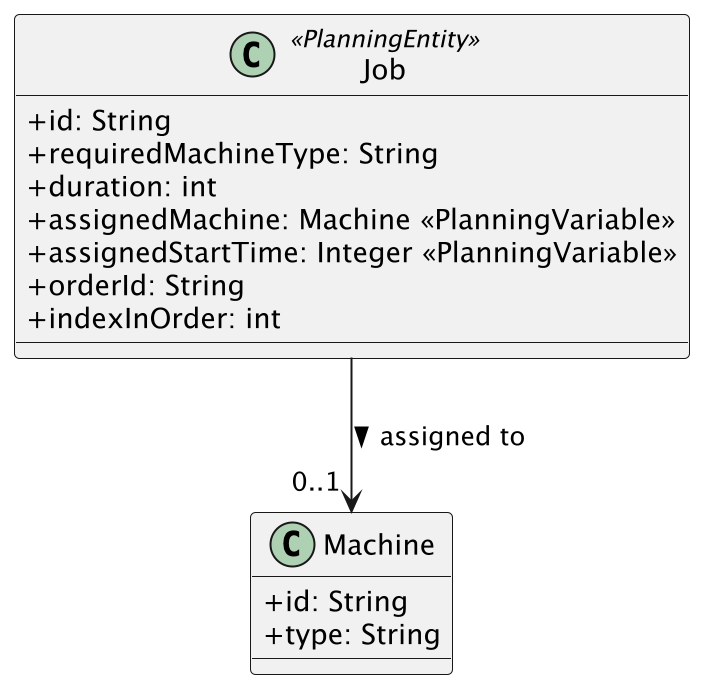
Im folgenden Beispiel verwende ich die Klassen Job und Machine. m folgenden Beispiel steht Job für einen einzelnen Arbeitsschritt innerhalb eines Auftrags, der wiederum aus mehreren solcher Schritte besteht. Jeder Arbeitsschritt muss auf einer bestimmten Typ Maschine ausgeführt werden. Innerhalb eines Auftrags ist die Reihenfolge der Arbeitsschritte fest vorgegeben, die Herausforderung liegt also in der zeitlichen Planung und Maschinenzuweisung.

Das Problem lässt sich mit Timefold sehr natürlich beschreiben:

• Jobs sind die Planning Entities – sie müssen verteilt werden.
• Maschinen sowie mögliche Startzeitpunkte sind die Problem Facts – feste Rahmenbedingungen.
• Die Zuordnungen „Job → Maschine“ und „Job → Startzeit“ ist unsere Planning Variable.

Ziele und Constraints

Was macht einen guten Plan aus? Das bestimmen die Constraints. Timefold unterscheidet hier sogenannte Hard-Constraints von Soft-Constraints.

Hard-Constraints müssen zwingen erfüllt werden, bei Nicht-Erfüllung ist eine mögliche Lösung ungültig. In unserem Kontext gibt es eine ganze Reihe davon:

• Nur passende Maschinen für jeden Job
• Kein Maschinenkonflikt (zwei Jobs zur selben Zeit auf derselben Maschine)
• Reihenfolge der Jobs innerhalb eines Auftrag ist zwingend vorgegeben

Ein Beispiel für einen Hard-Constraint:

private Constraint matchingMachineType(ConstraintFactory factory) {
  return factory.forEach(Job.class)
                .filter(job -> !job.getRequiredMachineType()
                             .equals(job.getAssignedMachine().getType()))
                .penalize(HardSoftScore.ONE_HARD)
                .asConstraint("Matching machine type");
}

Stimmt der benötigte Maschinentyp für einen Job nicht mit dem Typ der zugeordneten Maschine überein, wird der Hardscore entsprechend “bestraft”.

Soft-Constraints sind Optimierungsziele, durch sie werden bestimmte Aspekte einer möglichen Lösung belohnt oder bestraft. Ein paar Beispiele wären:

• Aufträge sollen möglichst früh abgeschlossen sein
• Maschinen sollen gleichmäßig ausgelastet werden
• Wechselzeiten oder Rüstkosten sollen minimiert werden (wenn Arbeitsstationen umgebaut oder Werkzeuge gewechselt werden müssen)

Ein Beispiel für einen Soft-Constraint:

private Constraint totalMakespan(ConstraintFactory factory) {
  return factory.forEach(Job.class)
                .filter(job -> job.getAssignedStartTime() != null)
                .penalize(HardSoftScore.ONE_SOFT, Job::getEndTime)
                .asConstraint("Total makespan");
}

Für jeden Job wird sein Endzeitpunkt beim Softscore gewertet, je später die Jobs enden, desto schlecht wird die Lösung bewertet.

Mit Timefold definieren wir diese Regeln in einem ConstraintProvider:

public class ProductionConstraintProvider implements ConstraintProvider {
    @Override
    public Constraint[] defineConstraints(ConstraintFactory factory) {
        return new Constraint[] {
                matchingMachineType(factory),
                noOverlapOnSameMachine(factory),
                processOperationsInSequence(factory),
                totalMakespan(factory)
        };
    }
    ...
}

Berechnen der Lösung

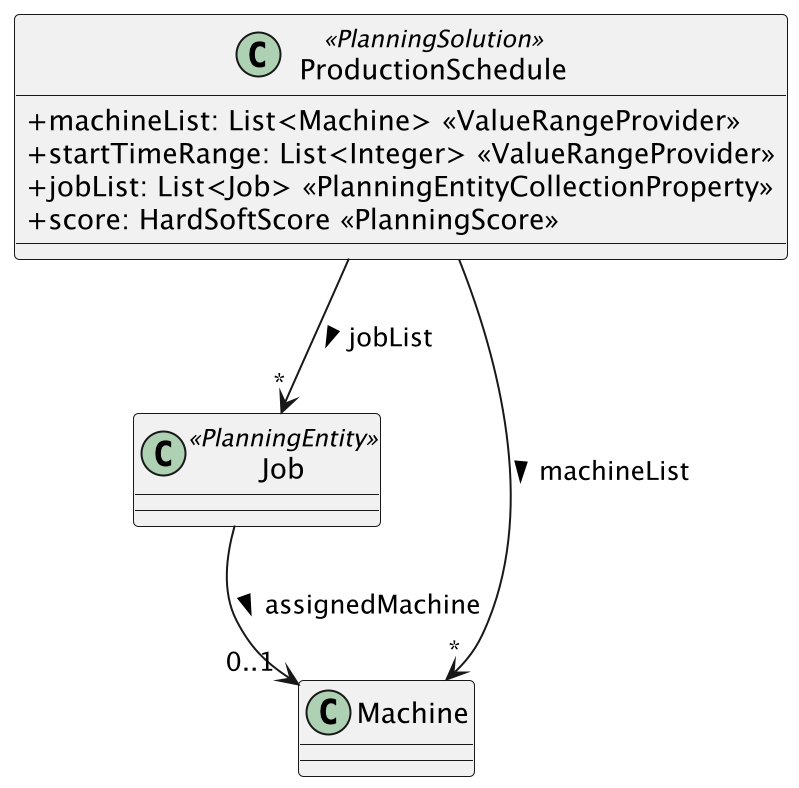
Jetzt müssen wir die bisherigen Teile noch zusammenfügen und daraus eine möglichst gute Lösung berechnen. Unsere Inputs (Maschinen und Zeitpunkte) sowie zu planenden Jobs fassen wir in einer Klasse ProductionSchedule zusammen, eine Art Stundenplan für unsere Produktion. Sie erhält die Annotation @PlanningSolution und enthält außerdem noch ein Attribut score vom Typ HardSoftScore. Dieser enthält die Bewertung der gerade betrachteten Lösung, intern besteht sie aus zwei Werten:

• hardScore: -1 für jeden verletzten Hard-Constraint, nur Lösungen mit hardScore 0 sind überhaupt gültig
• softScore: -1 für jedes penalize oder +1 für jedes reward, je höher, desto besser ist die Lösung

Jetzt sind wir bereit für die Durchführung der Berechnung. Dazu initialisert man ein ProductionSchedule Objekt und übergibt es zur Lösung an einen SolverManager. Der SolverManager ist eine Möglichkeit, um Timefold in einer produktiven Anwendung (z. B. ein Microservice-Backend) zu verwenden.
Er verwaltet Solver-Instanzen, sorgt für Thread-Sicherheit und ermöglicht, mehrere Optimierungen parallel und unabhängig voneinander laufen zu lassen. Man kann sich ihn vorstellen wie eine Steuerzentrale für Solver-Jobs.

private final SolverManager<ProductionSchedule, Long> solverManager;

public void compute() throws ExecutionException, InterruptedException {

    ProductionSchedule problem = loadProblem();
    var solverJob = solverManager.solve(1L, problem);

    printSolution(solverJob.getFinalBestSolution());
    printByMachine(solverJob.getFinalBestSolution());
}

Für einen Test nutzen wir ein kleines Beispielproblem.

Wir haben 4 Maschinen:

• M1 und M3 sind Pressen
• M2 ist eine Schleifstation
• M3 ist eine Lackierstation

Wir haben 3 Auftrage mit :

• O1 mit den Jobs J1 (Pressen, Dauer 1), J2 (Schleifen, Dauer 3), J3 (Lackieren, Dauer 2)
• O2 mit den Jobs J4 (Pressen, Dauer 1), J5 (Schleifen, Dauer 3), J6 (Lackieren, Dauer 2)
• O3 mit den Jobs J7 (Pressen, Dauer 1), J8 (Lackieren, Dauer 1)

Die Berechnung mit den oben angegebenen Hard- und Soft-Constraints ergibt dann beispielsweise den folgenden Produktionsplan:

Machine	Type	0	1	2	3	4	5	6	7	8	9
M1	PRESS	J7	J4
M2	GRIND		J2	J2	J2	J5	J5	J5
M3	PRESS	J1
M4	PAINT		J8			J3	J3		J6	J6

Es ist ganz interessant die Hard-Constraints auszukommentieren und dann nacheinander wieder zu aktivieren. Man wird sehen, wie nach und nach völlig unsinnige Lösungen (alle Jobs auf Maschine 1 und Startzeit 0) zu einer stimmigen Planungslösung werden.

Den Code zu diesem Teil findet Ihr hier auf Github. Wenn Sie Produktionsplanung in Ihrem Unternehmen optimieren möchten – sprechen Sie mich gerne an.

Der nächste Teil wird sich mit einer ganz anderen Problemstellung befassen. Es geht um Securitisation (Verbriefung), konkret um die sinnvolle Bündelung von Forderungen in handelbare Portfolios.