Teil 2 der Serie „Optimierungsprobleme in der Praxis“
In dieser Serie zeige ich, wie sich reale Planungs- und Entscheidungsprobleme mit modernen Optimierungstools wie Timefold elegant lösen lassen – praxisnah, reproduzierbar und mit klarem Mehrwert für Unternehmen.

Warum Securitisation Optimierung braucht
In der Finanzwelt bezeichnet man als Verbriefung (englisch Securitisation) die Bündelung vieler einzelner Kredite in handelbare Portfolios. Diese Portfolios können anschließend an Investoren weitergegeben werden, die abhängig von der Zusammensetzung unterschiedliche Risiken und Renditen abbilden.
In der Realität ist das ein komplexer Prozess mit vielen rechtlichen, bilanziellen und regulatorischen Anforderungen. Für unser Beispiel konzentrieren wir uns aber auf den Kern der Planungsaufgabe: Wie lassen sich Kredite so auf mehrere Portfolios verteilen, dass bestimmte Vorgaben eingehalten werden?
In unserem vereinfachten Modell gibt es:
- drei Portfolios mit unterschiedlichem maximalem Volumen
- eine Menge von Krediten mit unterschiedlichen Laufzeiten, Zinssätzen und Ratings
- die Bedingung, dass das maximale Volumen eines Portfolios nicht überschritten werden soll
- die Bedingung, dass das maximale Volumen eines Portfolios möglichst erreicht werden soll
- die Bedingung, dass jedes Portfolio nur Kredite mit einem Rating zwischen AAA und B enthalten darf
- und die Bedingung, dass mindestens die Hälfte aller Kredite eines Portfolios ein gutes Rating (AAA, AA oder A) haben sollen
Ziel: Kredite so auf 3 Portfolios verteilen, dass (a) Volumenlimits eingehalten, (b) möglichst ausgeschöpft und (c) mind. 50 % Investment-Grade pro Portfolio erreicht werden. Dieses Problem lässt sich nicht mehr durch einfaches Probieren lösen – die Zahl möglicher Kombinationen wächst exponentiell mit der Anzahl der Kredite. Genau hier hilft wieder ein Solver wie Timefold: Er findet in kurzer Zeit eine Lösung, die alle Randbedingungen erfüllt und das gewünschte Gleichgewicht zwischen Risiko und Verteilung herstellt.
Das Modell in Timefold
Um das Problem in Timefold abzubilden, benötigen wir nur wenige zentrale Klassen. Im Kern geht es darum, Kredite (Loans) auf Portfolios zu verteilen. Jeder Kredit hat dabei feste Eigenschaften, die vom Solver nicht verändert werden dürfen, das sind die sogenannten Problem Facts. Die Zuordnung zu einem Portfolio dagegen ist die Planungsvariable.
In unserem Beispiel sieht das Modell so aus:
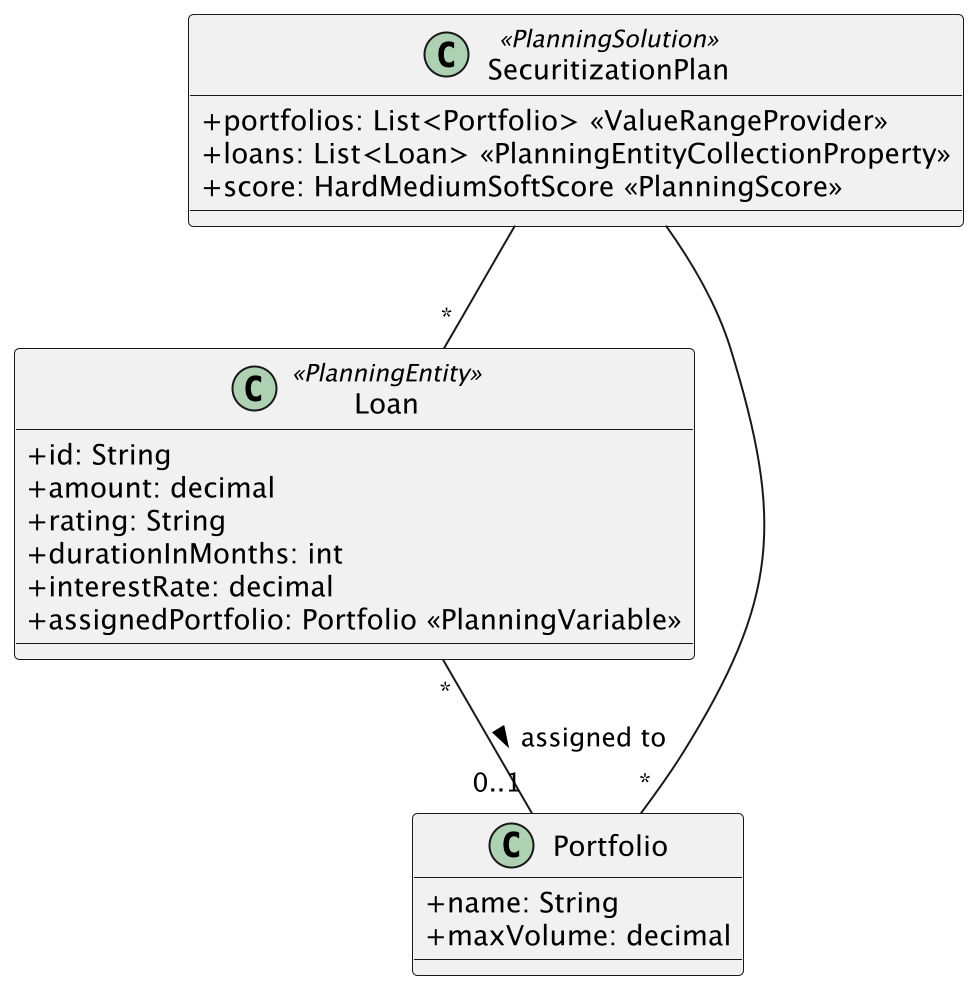
Loan
Enthält Attribute wie Kreditbetrag (amount), Zinssatz, Laufzeit und Rating (AAA … B). Der Solver darf diese Werte nicht verändern, sie beschreiben lediglich die Eingangsdaten. Weiterhin enthält Loan die Planungsvariable assignedPortfolio. Diese wird vom Solver gesetzt und gibt an, zu welchem Portfolio der Kredit zugewiesen ist.
Portfolio
Hat eine Bezeichnung sowie ein festgelegtes maximales Volumen. Dieses darf durch die Summe der zugeordneten Kredite nicht überschritten werden.
SecuritisationPlan
Die Lösungsklasse, die eine Liste aller Kredite (Loans) und Portfolios (Portfolios) als Input erhält. Weiterhin enthält sie die Bewertung (score), die der Solver optimiert. Im letzen Artikel haben wir zur Bewertung den Typ HardSoftScore verwendet. Im neuen Beispiel werden wir die Variante HardMediumSoftScore verwenden. Dieser ermöglicht drei Ebenen der Bewertung in Constraints:
- Hard Constraints müssen für gültige Lösungen erfüllt sein
- Medium Constraints bilden eine Art Zwischenebene. Anders als die Hard Constraints müssen sie nicht zwingend erfüllt werden. Aber sie sind wichtiger als die Soft Constraints und werden bei der Optimierung entsprechend berücksichtigt
- Soft Constraints bilden die schwächste Ebene. Aber innerhalb gleichwertiger Lösungen bezüglich der Hard und Medium-Constraints wird über die Soft-Scores optimiert
Die Constraints
Die eigentliche Logik des Problems steckt in den Constraints, die wir in der Klasse PortfolioConstraintProvider definieren. Hier sind die Constraints im Überblick:
- Hard Constraint: Maximalvolumen pro Portfolio
- Hard Constraint: Rating-Beschränkung (nur AAA bis B)
- Medium Constraint: Mindestens 50 % der Kredite pro Portfolio müssen ein gutes Rating (AAA, AA, A) haben
- Soft Constraint: Volumen möglichst nahe am Maximum
Diese Constraints sorgen dafür, dass der Solver nur zulässige Lösungen in Betracht zieht und gleichzeitig versucht, die Volumina der Portfolios optimal auszunutzen und möglichst das Kriterium “50% gutes Rating” zu erfüllen.
Im Prinzip sind die Constraints relativ ähnlich zu denen aus dem vorherigen Artikel. Auf zwei Besonderheiten möchte ich aber noch einmal eingehen:
private Constraint doNotExceedMaxAmount(ConstraintFactory factory) {
return factory.forEach(Loan.class)
.groupBy(Loan::getAssignedPortfolio, ConstraintCollectors.sumBigDecimal(Loan::getAmount))
.filter((portfolio, total) -> total.compareTo(portfolio.getMaxVolume()) > 0)
.penalize(HardMediumSoftScore.ONE_HARD)
.asConstraint("Portfolio volume exceeded");
}In diesem Constraint wird überprüft, ob das Gesamtvolumen der Kredite in einem Portfolio das maximale Volumen überschreitet. Dazu werden alle Kredite nach ihrem zugewiesenen Portfolio gruppiert und die Beträge summiert. Das funktioniert in etwa wie ein SQL mit GROUP BY und SUM(). Anschließend wird gefiltert, ob die Summe das Maximum überschreitet.
private Constraint atLeastHalfHighRatedLoans(ConstraintFactory factory) {
return factory.forEach(Loan.class)
.groupBy(Loan::getAssignedPortfolio,
ConstraintCollectors.count(),
ConstraintCollectors.sum(Loan::countAGrade))
.filter((portfolio, totalCount, investmentGradeCount) -> investmentGradeCount * 2 < totalCount)
.penalize(HardMediumSoftScore.ONE_MEDIUM, (portfolio, totalCount, investmentGradeCount) -> {
int fehlend = Math.ceilDiv(totalCount, 2) - investmentGradeCount;
return Math.max(fehlend, 0);
})
.asConstraint("Mindestens 50% A, AA oder AAA");
}In diesem Constraint wird überprüft, ob mindestens die Hälfte der Kredite in einem Portfolio ein gutes Rating haben. Hieraus hätte man einen Hard-Constraint machen können, damit diese Bedingung zwingend erfüllt wird. Eventuell ist es (abhängig von den verfügbaren Krediten) nicht möglich, diese Bedingung zu erfüllen und wir wollen nur nahe genug an das Ziel herankommen. Trotzdem wiegt dieses Ziel mehr als die maximale Ausnutzung des Portfoliovolumens (Soft-Constraint).
Der Constraint ist auf den ersten Blick vielleicht nicht ganz einfach zu verstehen.
- Zunächst wird nach den Portfolios gruppiert und die Gesamtanzahl der Kredite sowie die Anzahl der “guten Kredite” je Portfolio ermittelt
- dann werden nur die Portfolios herausgefiltert, bei denen die “guten Kredite” weniger als 50% ausmachen
- diese erhalten eine “Bestrafung” abhängig von der Abweichung vom anvisierten Anteil von 50% (totalCount / 2)
Berechnung der Lösung
Jetzt geht es wieder an die Berechnung der Lösungen. Dafür verwenden wir wie im ersten Teil den SolverManager. Die Testdaten generieren wir in diesem Beispiel nach dem Zufallsprinzip, da wir für einen guten Test eine ganze Menge Kredite benötigen.
private SolverManager<SecuritisationPlan, Long> solverManager;
public void compute() throws ExecutionException, InterruptedException {
SecuritisationPlan problem = loadProblem();
var solution = solverManager.solve(1L, problem);
printPortfolioSummary(solution.getFinalBestSolution());
logger.info("Solution score: {}", solution.getFinalBestSolution().getScore());
}
private SecuritisationPlan loadProblem() {
List<Portfolio> portfolios = TestDataGenerator.generatePortfolios();
return new SecuritisationPlan(
portfolios,
TestDataGenerator.generateLoans(1000, portfolios));
}
Die Berechnung ergibt dann zum Beispiel die folgende Lösung:
| Name | Max Volume | Total count | A Grade | B Grade | Volume |
| Portfolio A | 100.000.000 | 35 | 20 | 15 | 99.999.489 |
| Portfolio B | 75.000.000 | 30 | 19 | 11 | 74.999.648 |
| Portfolio C | 50.000.000 | 20 | 10 | 10 | 49.999.476 |
Man kann erkennen, das die Volumina der verschiedenen Portfolios gut ausgeschöpft werden. Weiterhin können wir sehen, dass der Constraint bezüglich der A Grade Kredite erfüllt wurde. Auch hier lohnt es sich wieder mit dem Code zu experimentieren. Zum Beispiel kann man die Erzeugung der Beispieldaten anpassen. Man könnte mehr Kredite mit kleineren Summen verproben oder absichtlich Konstellationen erzeugen, bei denen der 50%-Constraint nicht mehr vollständig erfüllt werden kann.
Den Code zu diesem Teil findet Ihr wieder hier auf Github. Wenn Sie ähnliche Probleme in Ihrem Unternehmen optimieren möchten – sprechen Sie mich gerne an.